Refresh your memory on how to teach long division with success for students and yourself. This step-by-step guide is filled with tips and helpful advice.
So many teachers become frustrated while teaching students how to solve long-division problems. I know that feeling well; I’ve been there. But teaching long division doesn’t have to be as difficult as that – cross my heart!

I’ll walk you through a few steps that make long division easier for you to teach. But first, let’s talk to our students about what long division is and why it exists in the first place.
Introduce the topic to students.
As you’re introducing long division to students, setting the right tone is important. They shouldn’t be told how hard it is or that it’s scary and tough to learn. They need reassurance and confidence that they’ll be successful with your help.
Say something like, “I know you’re excited to learn about long division. We’ll use many skills you’ve learned over the years and put them together to solve division problems.”
Go on to explain that long division is simply a way of splitting a number into smaller, even parts. In real-life terms, it’s a way of dividing a big group of things into many smaller groups.
For example, if we have a bag of candies and a group of children. We want each child to get the same number of candies, so we need to figure out how many candies each child gets. We can find the answer through long division.
Teach the basic terminology.
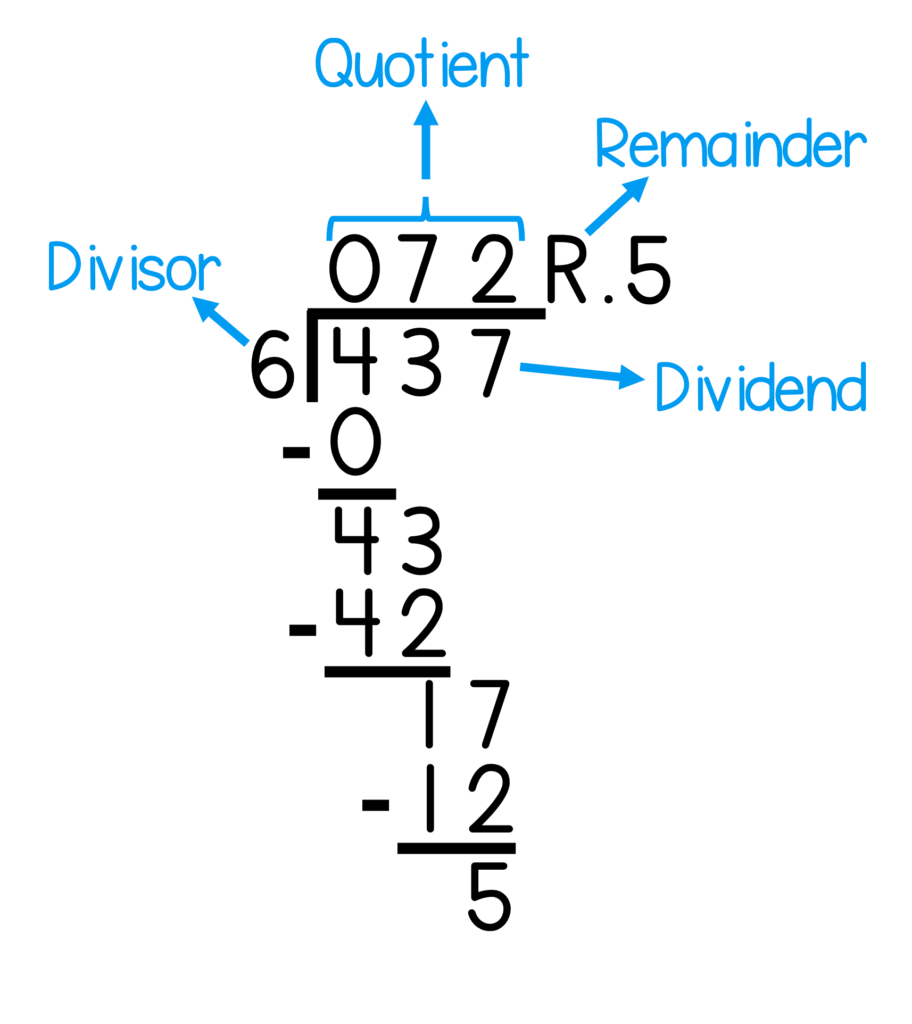
While instructing students, you should use the correct terminology. Here’s a quick refresher:
- The dividend is the number being divided or split up (the number inside the division symbol).
- The divisor is the number you divide by (the number of groups the dividend is split into).
- The quotient is the name of the answer to the division problem (how many are in each group).
- The remainder is the number that is left over after dividing.
In other words, dividend ÷ divisor = quotient, and the remainder is any extra amount.
You may have to provide several more examples to help students understand why we perform long division.
Long division can be broken down into steps.
Long division is a process that can be broken down into steps. Teaching each step will make it easier for students to become fluent. Long division takes practice, repetition, and feedback, but students will master the skill over time.
As you begin to instruct students on the steps for solving long division, follow these steps:
1. Set up the equation with a dividend and divisor.

2. Divide the first digit in the dividend by the divisor by finding how many times the divisor can go into the first digit of the dividend. Write that number above the first digit of the dividend. That is the first digit of the quotient. In the above example, ask how many groups of 5 are there in 3?
3. If the divisor is larger than the first digit, place a zero above the first digit of the dividend
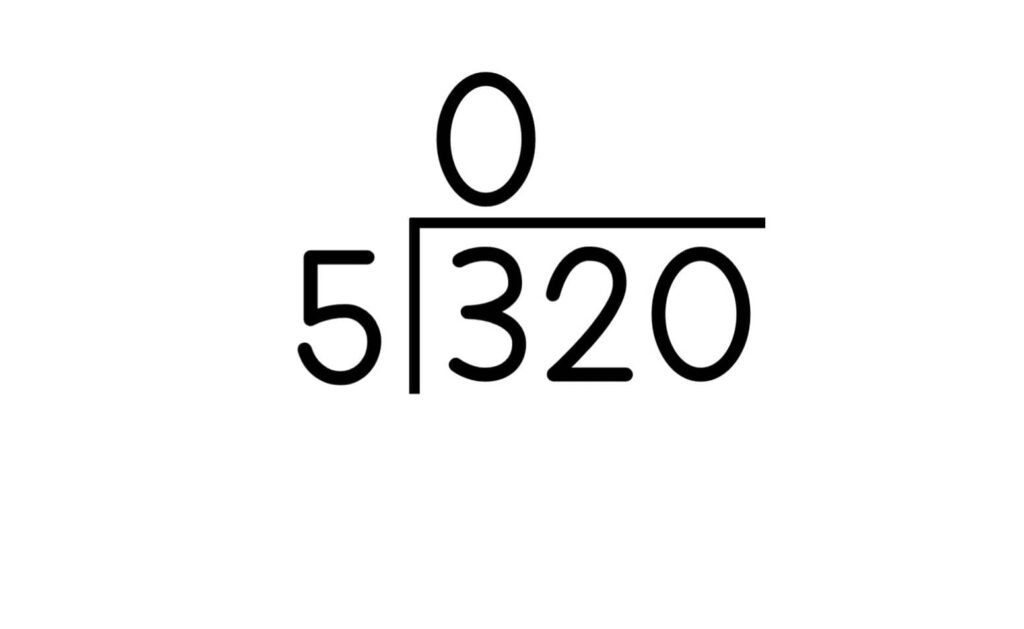
4. Multiply the digit in the quotient times the divisor. In our example, this is 0.
5. Write the product below the dividend.
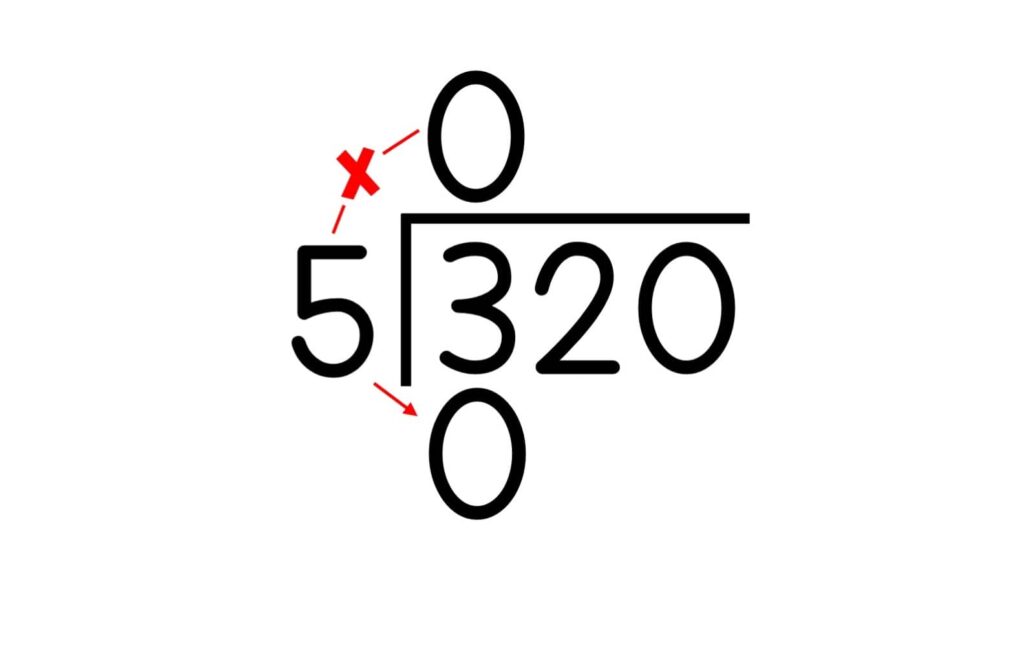
6. Write a line under the product.
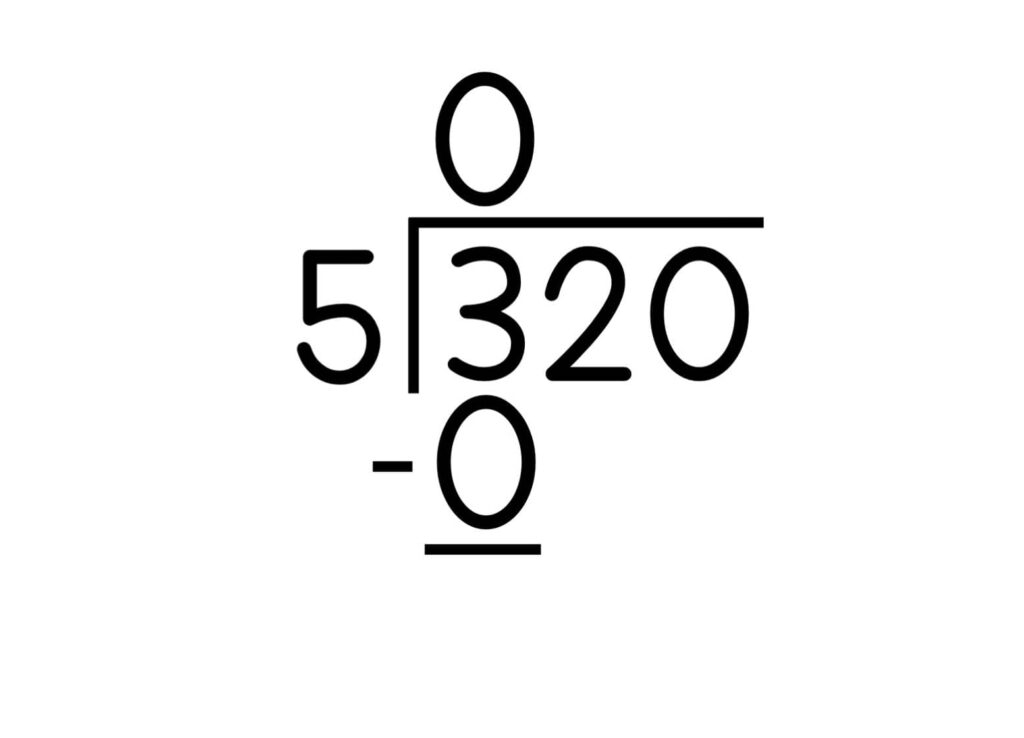
7. Subtract the product from the dividend. Write the difference (answer) under the line.
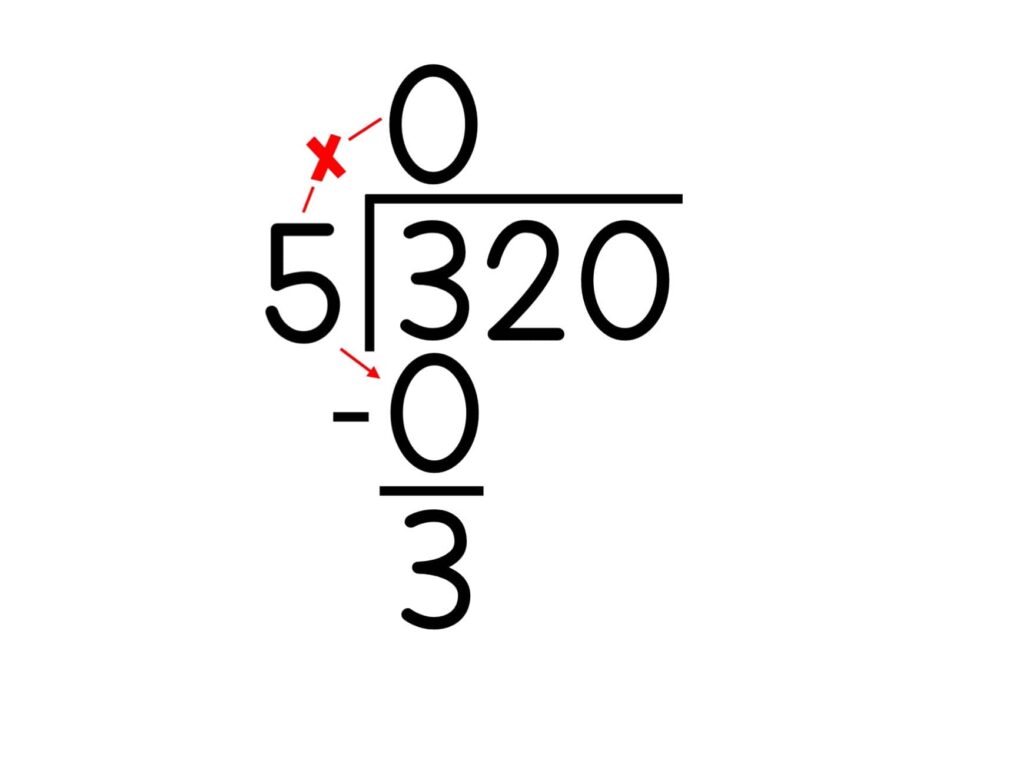
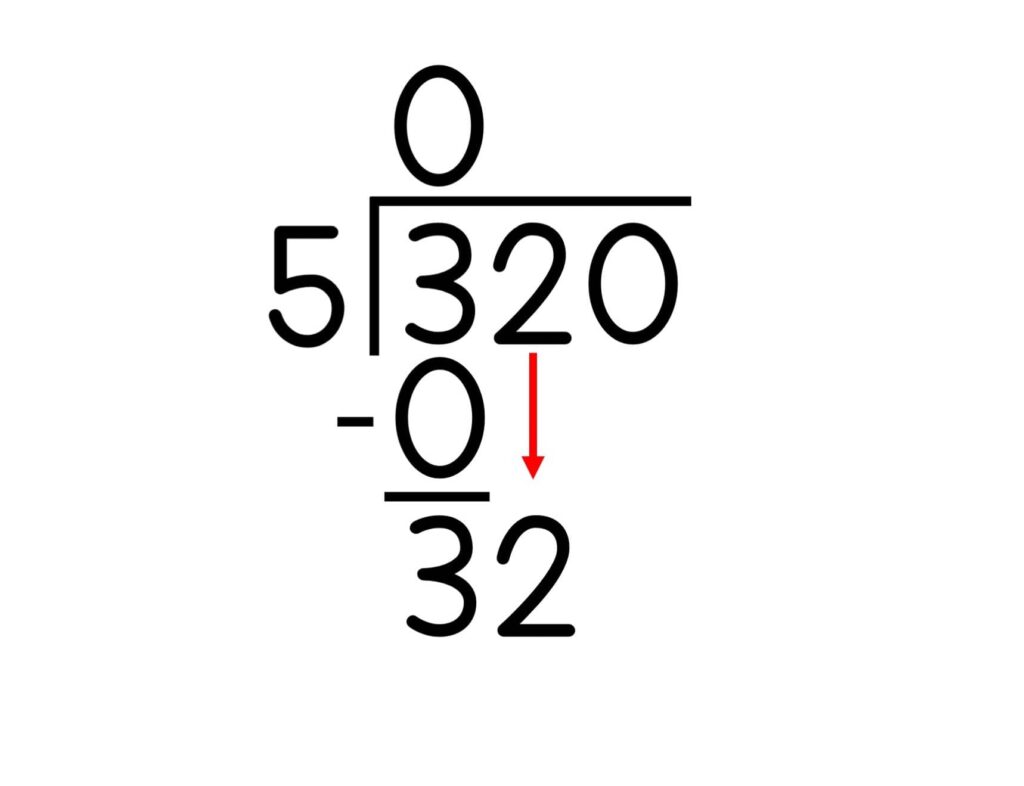
8. Bring down the next digit in the dividend.
9. Repeat the process by dividing the new number by your divisor. Write that digit above the dividend as the next digit of the quotient. Continue this process until all the digits in the dividend have been brought down and divided.
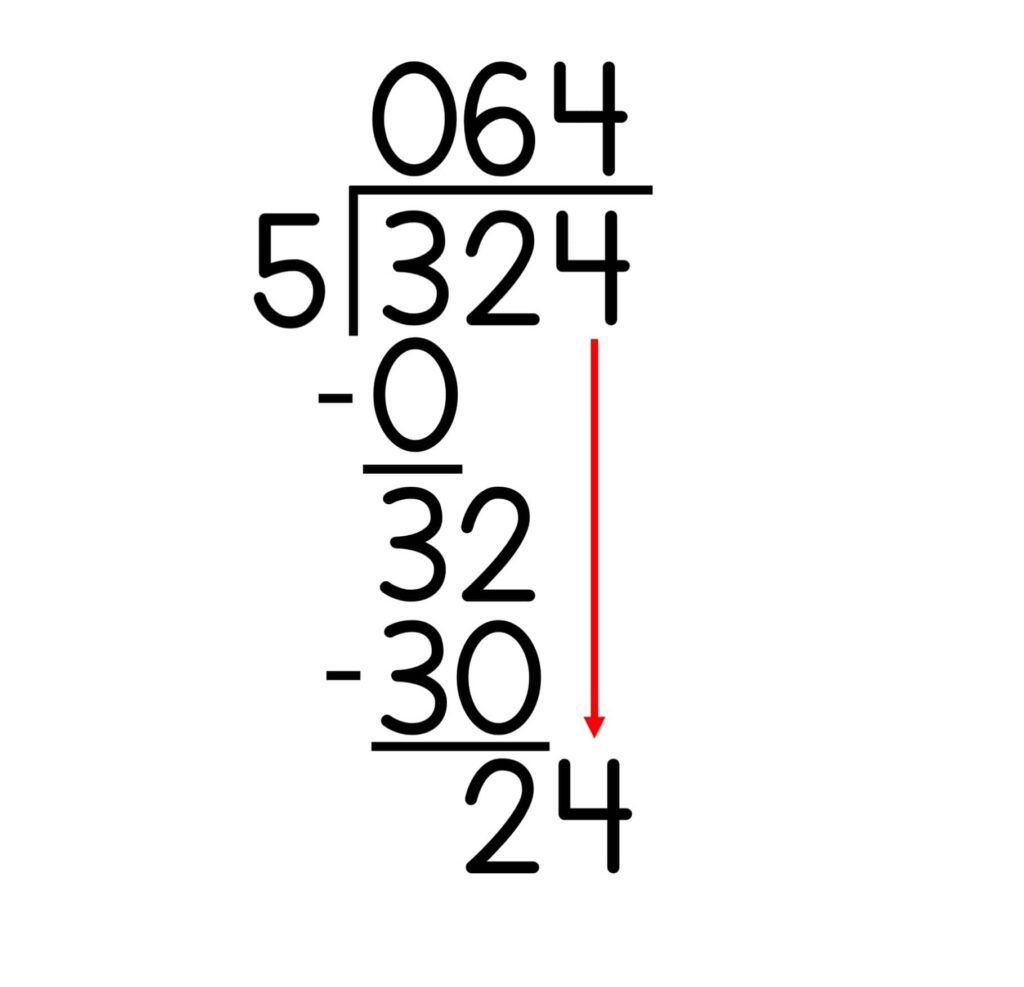
10. If the numbers don’t divide evenly, you’ll be left with a remainder. After the quotient, write “R.” and then the number left over. In our example, that remainder is 4.
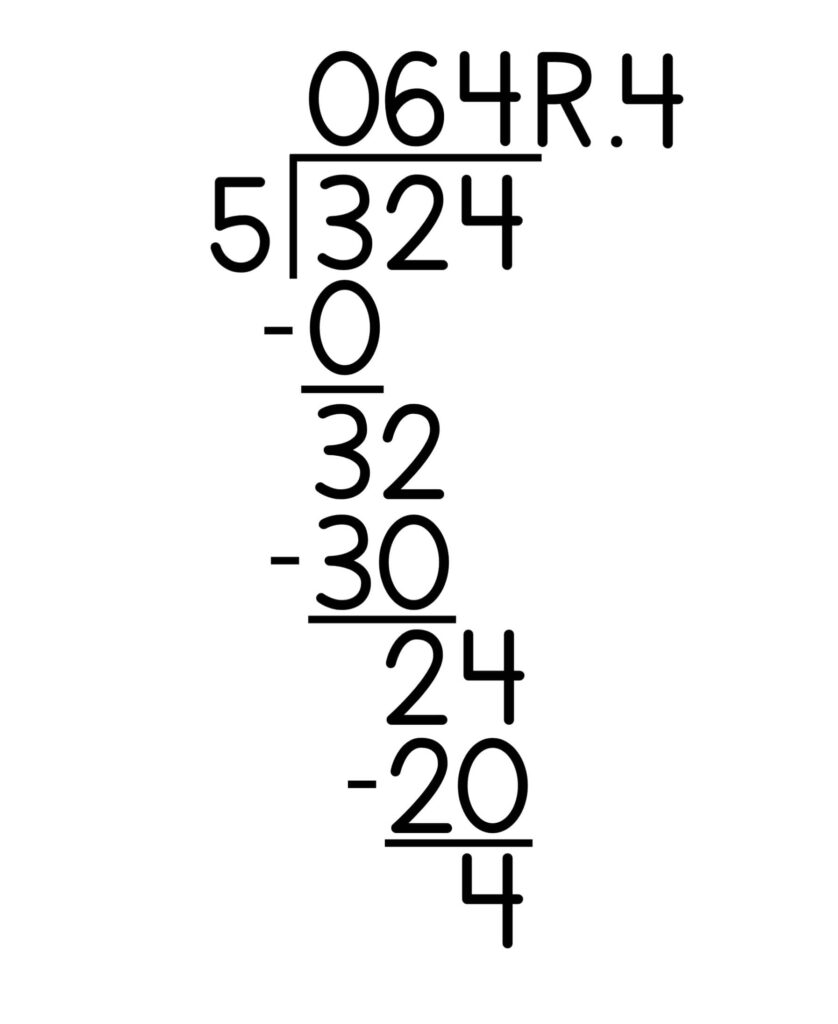
11. Remember to label your quotient and final answer. If you divide candies between children, you’ll label the final answer “candies.”
Provide several examples and think out loud.
Students learn a lot by hearing how you problem solve.
As you’re explaining the examples, be sure to model your thinking out loud. For example, you might say, “Hmm. How many groups of 7 can be taken out of 30? I know 7 x 4 is 28, and that’s pretty close to 30.”
Be sure to:
- Over-teach by providing plenty of examples.
- Explain your thinking and reasoning for each step of the process.
- Be consistent. Repeat the process the same way every time.
- Provide real-world examples to help students understand how we use division in real-life situations.
- Use visual aids such as anchor charts, reference guides, posters, and diagrams to illustrate the concepts.
- Provide frequent feedback. The more often you provide feedback, the more students can self-correct.
Practice, practice, practice in a group.
Provide a long division problem for students to solve at their seats using whiteboards or paper. Have students practice problems independently or with assistance from a partner. As students are working, circulate around the room to provide frequent feedback. Once most students are finished, invite a student to show their work as they solve the problem in front of the class. Sometimes hearing the steps from a peer helps students understand. Discuss problem areas before moving on to the next problem.
As you’re circulating around the room, if you see students having trouble, ask them questions about their thinking processes. Make corrections on the spot to ensure that students understand the steps.
You can also have students use their whiteboards for questions about what they don’t understand.

More about partner work.
Partner work with whiteboards is a great way for students to learn from each other. Plus, they can check each other’s work while practicing to improve their skills. Teaching others is the highest form of understanding, so students who are comfortable with the process can help classmates who are still struggling. Both students benefit.
Important note – Peer tutoring can be a valuable part of learning for both students. However, don’t overuse it. Advanced students should be challenged so they continue moving forward. Struggling students need direct instruction from trained teachers. Use this approach wisely.
During partner work, you can circulate around the room and catch students’ mistakes immediately. The immediate feedback and reinforcement save students time and frustration.
Be sure to note the students who need more assistance. You can work with those individuals in a small group or individually.
My favorite method for teaching long division.
My absolute favorite method for teaching long division is Shaped Math. It’s fantastic for introducing long division and for students who need support.
Check out the video that explains this visual support for teaching long division.
Grab This FREE Long Division Set:
Grab the FREE Shaped Math Long Division.

Learn more about How to Teach Long Division with Shaped Math.
Additional tools to support students:
For students who need additional support, try out graph paper accommodations.
Standard Algorithm Using Shaped Math.
Conclusion.
Hopefully, you’ve found these tips helpful. If you’re teaching long division, this strategy is a great way for students to learn the skill successfully.